Settings steganography
July 16, 2025 at 12:10 PM by Dr. Drang
Last week, I was going to be out with my MacBook Pro all day, and I wanted to make sure it was fully charged. I had noticed that it was typically charging up only to about 80%, and I assumed that was because Sequoia was doing some clever battery-life-lengthening thing. I wanted to turn the clever thing off so I could get the battery to 100% just for that day.
You will probably not be shocked to hear that I didn’t find the solution by simply opening System Settings and scanning the Battery panel—I had to do a Kagi search for it. It wasn’t that the toggle was buried several layers deep or that it was outside the Battery hierarchy. No, the problem was that Apple had put the toggle in a place where toggles—or any kind of control or data entry field—don’t belong.
Here’s the Battery settings panel:
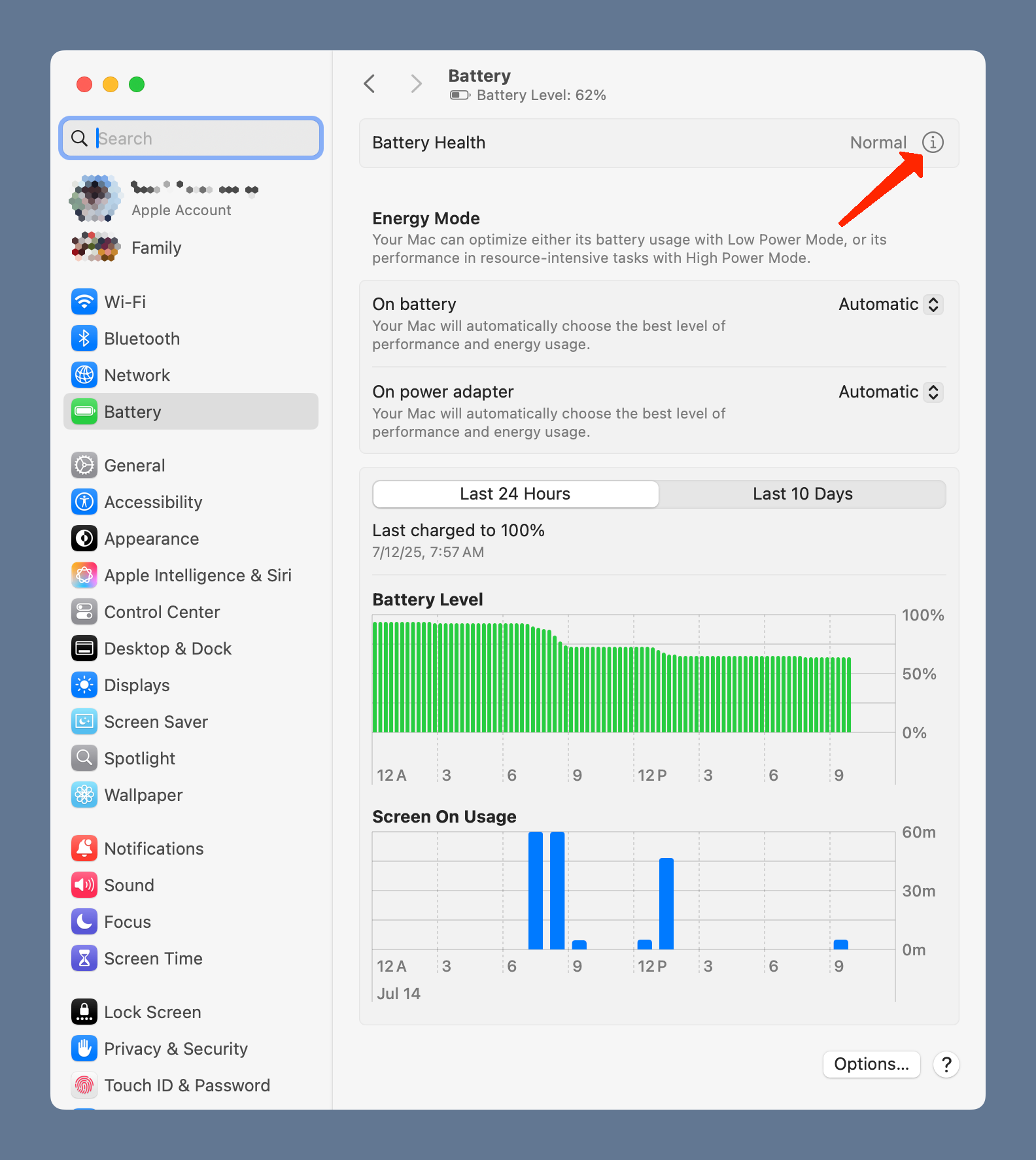
The two popup menus in the Energy Mode section of the panel aren’t what I wanted, so I assumed the setting for turning off battery optimization would be found via the button down at the bottom of the panel. But it wasn’t in the window that appeared when I clicked it.
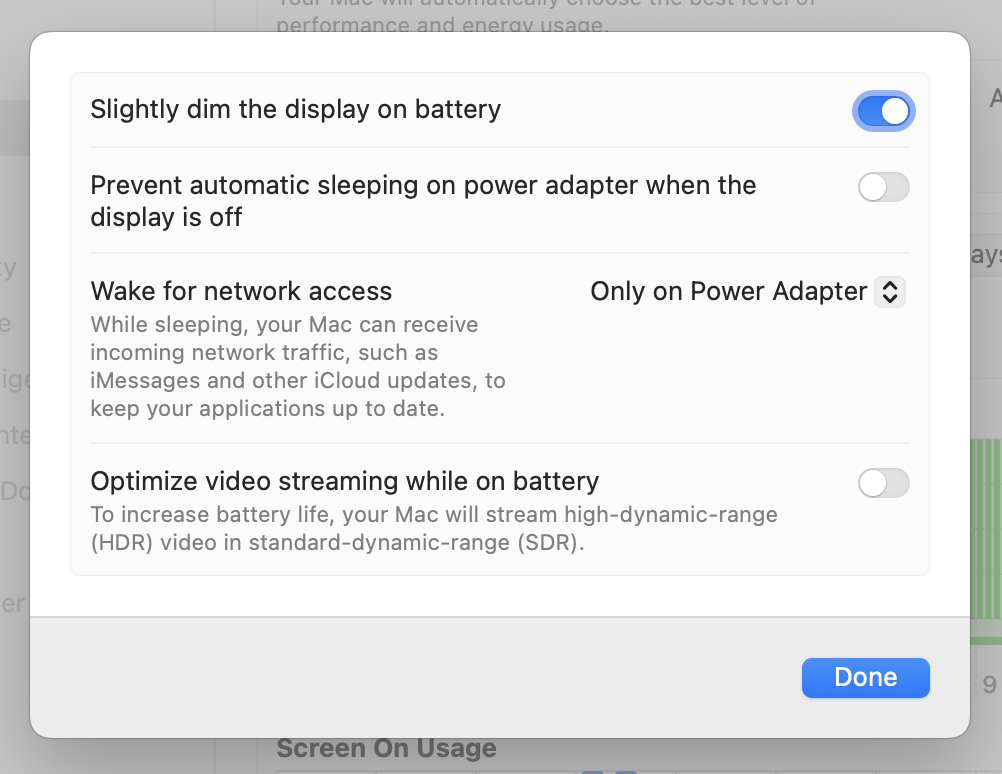
Well, I’ve already given away the secret with the red arrow in the first screenshot. You have to click the ⓘ button near the top right corner. That brings up this window with the toggle I was looking for.
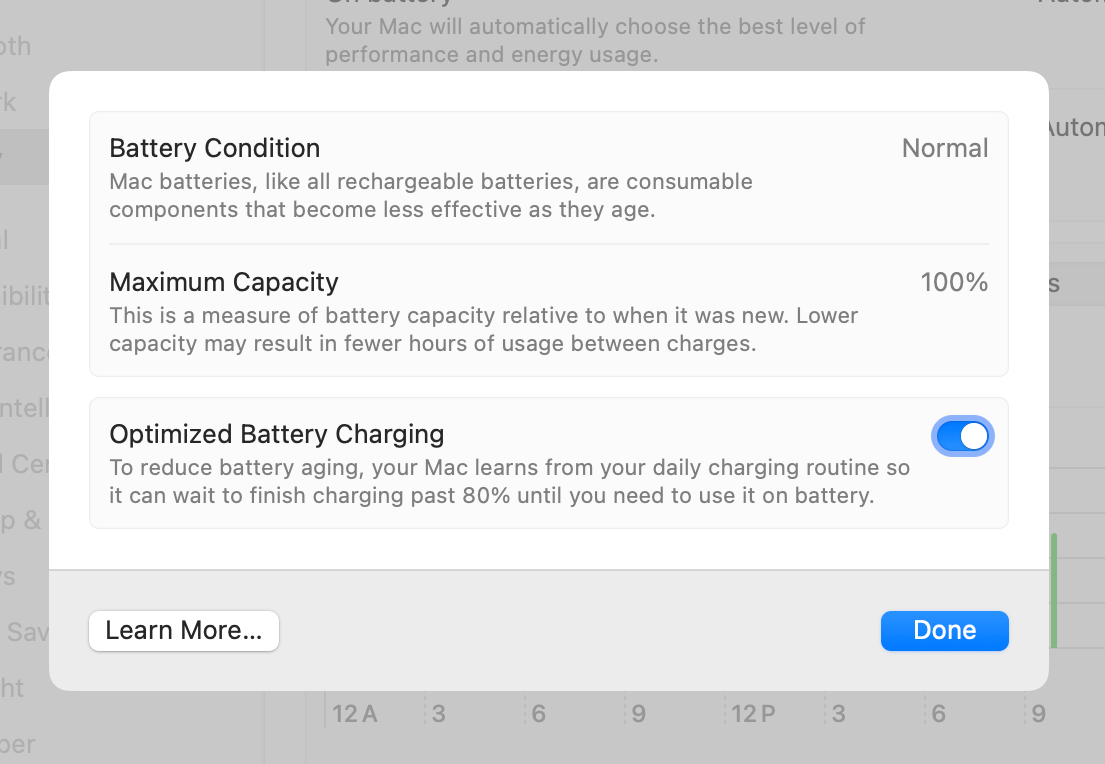
Turning the toggle off brought up this further set of options:
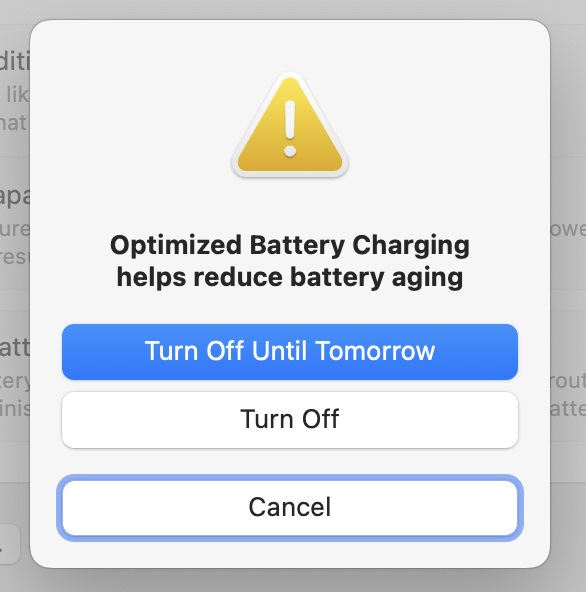
Before I start complaining, let me say this final dialog box is nice. You can turn off optimized charging permanently if you want, but the default is to just turn it off for a day. The clear implication is that Apple thinks you should use non-optimized charging rarely, and it will help you turn it back on tomorrow if you forget.
Now for the complaint: none of this should be behind the ⓘ button. The “i” clearly means “information,” and when I click on it, I expect to be given information, not to give it. Just as you wouldn’t put toggles or other controls behind the ?⃝ button, you shouldn’t put them behind the ⓘ.
I know there’s always talk of Apple losing its way in user interface design. And that talk has been especially loud since the release of the xxxOS 26 betas. My Mastodon timeline has been filled with criticism of Liquid Glass and Alan Dye for weeks, and it’s tiresome to read the constant grousing. But then I run into this, and I need to do some grousing myself.
When Venus is in the House of Games
July 7, 2025 at 1:01 PM by Dr. Drang
I had a touch of insomnia last night and tried to cure it by watching YouTube videos. The algorithm suggested a compilation of quiz questions from Richard Osman’s House of Games, a British game show that I used to watch regularly back in 2020, when I was trying to take my mind off of things I had no control over.
The cure didn’t work, because the video I watched was this one, and the last question—which starts at about the 26:35 mark—gave what I was sure was the wrong answer. So instead of falling asleep, I went off to look up the right answer and then got caught up in how to calculate it.
The question was “How many hours are there in one day on the planet Venus?” and the answer they gave was 5,832. Now, I am by no means an expert on Venusian planetary motion. I know its year is somewhat more than 200 Earth days, that it rotates backwards, and that its days are quite long. But in my mind, “quite long” is nowhere near 5,832 hours.
So I went to NASA’s Venus Fact Sheet, which told me that its day is 2,802 hours, roughly half of what House of Games said. But the number 5,832 did appear in the section on Venus’s orbital parameters:
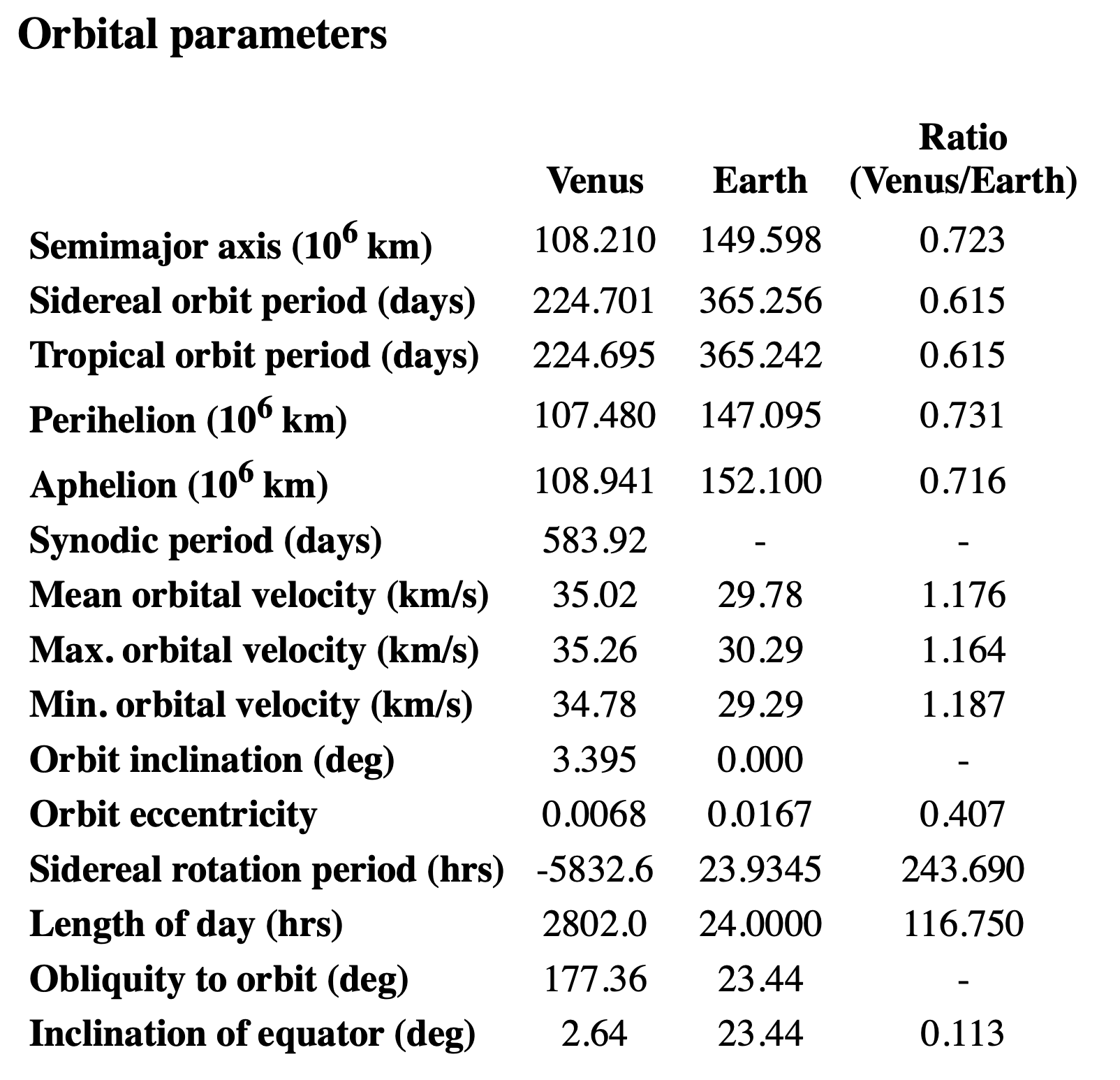
It’s fourth from the bottom in the row labeled Sidereal rotation period. I took the negative sign to be an indication of Venus’s backward rotation, similar to the obliquity being given as 177.36° instead of 2.64°.
(By “backward rotation” I mean that Venus rotates in the opposite direction of its revolution around the Sun.)
So now I felt compelled to figure out how the -5,832.6 hours of sidereal rotation related to the day length of 2,802.0 hours. Which kept me awake longer.
First, I noticed—or rather, PCalc told me—that the sidereal orbital period of 224.701 Earth days is 5392.824 hours, a number that’s fairly close (in magnitude) to the sidereal rotation period. I imagined looking “down” on a solar system in which a planet revolved counter-clockwise around its sun and rotated clockwise about its axis at the same speed. It would look like this at various points in its year:
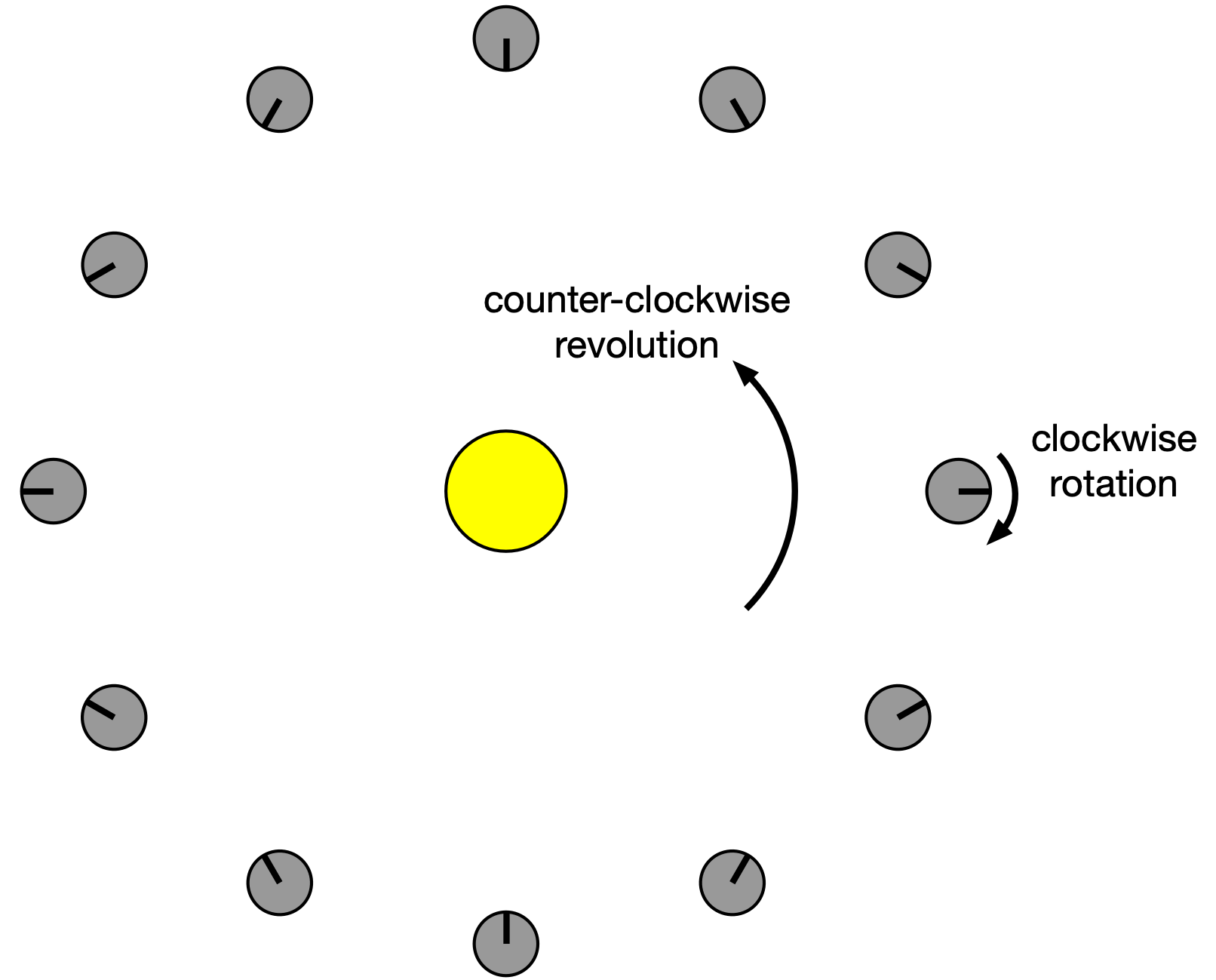
The black line on the planet is a meridional stripe that runs from pole to pole to help see the rotation. For every 30° of counter-clockwise revolution of the planet about its sun, there is 30° of clockwise rotation about its axis. This is all relative to us, who are looking at this from the point of view of the stars (sidereal).
As you can see, midnight to midnight on the planet’s meridional stripe takes half a year. That’s going from the 3:00 position around to the 9:00 position. So for these conditions—a planet rotating clockwise at the same speed it revolves counter-clockwise—there will be two days in a year.
So in rough numbers, there are two Venusian days in a Venusian year. With a Venusian year being about 5,400 hours, that makes its day about 2,700 hours long. But let’s do a more precise calculation to see if we can get all the numbers in the fact sheet to line up.
Taking Venus to move in a circular orbit, its orbital speed is
Its rotational speed about its axis is
So Venus will have gone through one day when
That works out to
or
which matches the value in the table.
This correct answer, by the way, would not have changed who got the points in the game. Both teams were orders of magnitude too low. And with my curiosity satisfied and my phone turned off, I went back to sleep.
Make no AI plans
July 4, 2025 at 4:26 PM by Dr. Drang
A couple of weeks ago, I asked ChatGPT to plan a driving route for me to visit all the Louis Sullivan jewel box banks. My goal was to make an Apple Note with all the banks and their Apple Maps links so I’d have everything I needed in a single document, but I didn’t have time right then to make the Note, so I put it aside without looking at it carefully. Today I went back to the ChatGPT conversation to pull out the information and found—well, you can probably guess what I found: one major mistake and a couple of minor ones. Enough errors that I ended up writing the Note without copying any of the info ChatGPT gave me.
Here’s ChatGPT’s unnecessarily verbose introduction to the route it planned:
The eight “jewel box” banks designed by Louis Sullivan are located in the Midwest, primarily in Iowa and Illinois. To visit them all, a logical route can be planned to minimize driving distances. Here’s an optimized route starting and ending in Chicago, Illinois, for convenience:
To its credit, ChatGPT did get the number of jewel box banks correct, even though I didn’t include that in my request. However, the “primarily in Iowa and Illinois” part is troublesome. Iowa is fine—there are three in that state—but Illinois? We’ll see about that later.
Here’s the list of banks in the order I’m supposed to travel:
- National Farmers Bank of Owatonna
101 N Cedar Ave, Owatonna, MN 55060 - Peoples Savings Bank
101 1st Ave SW, Cedar Rapids, IA 52405 - Henry Adams Building
124 E State St, Algona, IA 50511 - Merchants National Bank
833 4th Ave, Grinnell, IA 50112 - Home Building Association Company
23 S Park Pl, Newark, OH 43055 - Peoples Federal Savings and Loan Association
101 E Court St, Sidney, OH 45365 - Purdue State Bank
210 Main St, Lafayette, IN 47901 - Land Bank (Southwest State Bank)
331 E Monroe St, Springfield, IL 62701
Going from Grinnell, Iowa, to Newark, Ohio, makes for a long day of driving, so I doubt this is the “optimized route” ChatGPT claimed. At least it’s not optimized for the person doing the driving.
More important, though, is the last bank on the list, which is fictitious. There are no jewel box banks in Illinois. And as far as I can tell, there’s no bank of any kind at that address. Maybe ChatGPT got tired after getting seven out of eight right.1
The eighth jewel box bank is the Farmers and Merchants Union Bank in Columbus, Wisconsin. The Wikipedia pages for most of the other seven banks—Newark, Sidney, West Lafayette, Cedar Rapids, Grinnell, Algona, and Owatonna—have links to all the others, so it’s hard to imagine how ChatGPT messed this up.
While I’ve had some success with LLMs—and ChatGPT in particular—the successes have come with coding problems, where checking the results is easy and immediate: I just run the code generated for me and see if it works. Other errors take effort to find, and I’m finding that effort often greater than just doing all the work myself. This problem, for example, took basically just a couple of Kagi searches and then following the Wikipedia links. And I now have a Note with all the (correct) information I need.
One more thing: Don’t write to tell me that my title for this post is messed up. I know it was Daniel Burnham who said “Make no little plans,” not Louis Sullivan. I just couldn’t think of a good title based on “Form follows function.” And frankly, a Burnham/Sullivan mixup seems appropriate for a post about AI.
-
Close enough to right, anyway. The address it gave for the bank in Newark, Ohio, is wrong, but the real address is just around the corner. If you went to the ChatGPT-supplied address, you’d see the bank across the town square. ↩
Python, interactively
July 1, 2025 at 10:30 PM by Dr. Drang
I recently realized, after including code from interactive Python sessions in recent posts (this one and this one), that I have more to say about my use of the Jupyter console than I covered in this post back in December.
First, although the Jupyter console can run interactive sessions in Julia and R, I use it only for Python, which means I’m really working in IPython, which is what the Jupyter console runs by default. Here’s the startup message that appears after I run jupyter console in the Terminal:1
Jupyter console 6.6.3
Python 3.13.5 (main, Jun 11 2025, 15:36:57) [Clang 17.0.0 (clang-1700.0.13.3)]
Type 'copyright', 'credits' or 'license' for more information
IPython 9.3.0 -- An enhanced Interactive Python. Type '?' for help.
Tip: `?` alone on a line will brings up IPython's help
It displays the version numbers for Jupyter console, Python, and IPython. Everything after the Jupyter console version number is the IPython “banner.” The tip at the end varies from session to session.
So if all I’m really doing is running IPython, why not do so directly? It’s a good question, and one I don’t have an especially satisfactory answer to. I started using Jupyter with notebooks. When I decided I preferred working in a console session instead, I just stayed in the Jupyter environment out of habit. At the time, I probably thought it was different from IPython and possibly an improvement. Maybe confessing publicly to this lame reason will get me to shift to IPython directly. To start the ball rolling in that direction, I’ll just refer to IPython from now on.
If you look back at the startup message, you’ll see that I’m running Python 3.13. You may have heard that this version has improvements to its standard interactive environment. It does, but it still isn’t as nice as working in IPython, mainly because of the magic commands.
When I’m working on a Python script, I try to test all the code as I write it, Typically, this means writing the code in BBEdit, saving it to a file, and testing it in IPython. The magic commands %run and %reset are the keys to this workflow. Typing
%run script.py
in an IPython session runs all the code in the file and keeps the session active. I can then check on what’s been written so far: calling functions with a variety of inputs, inspecting the values of variables, making sure loops and conditionals work the way they’re supposed to.
After adding to or fixing the code, I return to the IPython session and type
%reset -f
This clears out all the names defined earlier in the session so the next %run starts fresh.
Because IPython keeps a history, I seldom have to type out %run script.py or %reset -f in full. Typing ⌃R puts IPython in an interactive backward search mode. Typing %ru after that brings up the most recent %run command; typing %re brings up the most recent %reset.
Even better—and this is a Bash tip, not an IPython tip—because I have these commands in my .bashrc file,
bind '"\e[A":history-search-backward'
bind '"\e[B":history-search-forward'
I can type %ru and then the ↑ to bring up the most recent %run command. Similarly with %re and ↑. I learned these bindings from a long-ago post by Craig Hockenberry and they work in all Terminal sessions, not just IPython.
(Depending on how you have things configured, IPython may show you the most recent matching command as soon as you start typing. These are called autosuggestions. I find the feature very annoying and don’t use it.)
The %rerun command can be useful when you have a handful of commands that you want to run again in the same order. For example,
%rerun -l 4
will rerun the last four commands. I confess I don’t use %rerun as much as I should. I tend to use ↑ to go back through the history again and again, only realizing after I’m done that I could’ve saved time using %rerun.
After %run and %reset, my most commonly used magic command is probably %history. Using it like this,
%history -opf session.txt
creates a file with all the input and output of the current session. The -o option tells it to include the output; the -p option tells it to put >>> in front of all the input lines, making it look like a regular Python interactive session (even though it wasn’t); and the -f <filename> option tells it where to save the output. You can also give it a range of session lines to print. This is what I did to create the interactive Python code I added to those recent posts.
Another %history option, helpful when you’re trying out code in an IPython session and finally hit upon what you want to add to your script, is -t. Using this without -p or -o will print out the session code in a format that can be pasted directly into your script.
Finally, IPython has several ways to incorporate previous output into a command. Suppose our session has gone like this:
In [1]: a = 1; b = 2; c = 3
In [2]: b*c
Out[2]: 6
In [3]: a + b*c
Out[3]: 7
In [4]: a + c**2
Out[4]: 10
At this point, we can multiply the third Out by c like this:
In [5]: Out[3]*c
Out[5]: 21
In and Out are not just labels, they’re Python variables that are continually updated during the session, and you can refer to them at any time. If typing Out and brackets is too much work (it is for me), you can use an underscore and a number to refer to previous output, e.g.,
In [6]: _4**c
Out[6]: 1000
This simplified way of referring to previous output is reminiscent of Python’s long tradition of using the underscore (all by itself) to refer to the most recent output in an interactive session. IPython follows that tradition and extends it: two underscores (__) refers to the second most recent output, and three underscores (___) refers to the third most recent output. But that’s where it stops—apparently the IPython developers consider four underscores beyond the pale.
I’m sure there are other things I do in interactive Python sessions, but these are the ones I use often enough to remember.
-
You may recall from the December post that I have
jupyter consolealiased tojcin my.bashrcfile, so I haven’t typed outjupyter consolein full in several years. ↩
